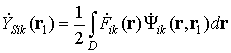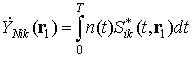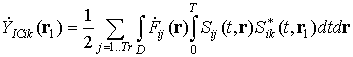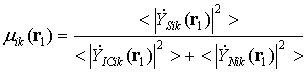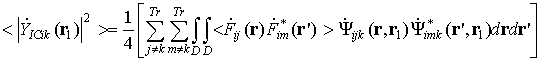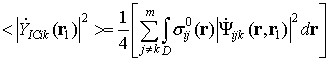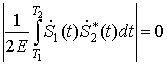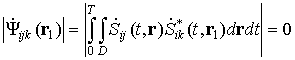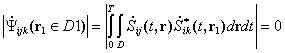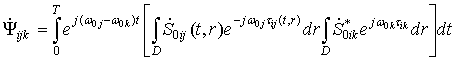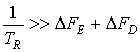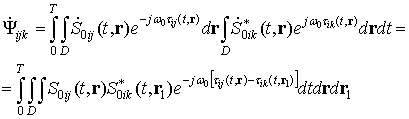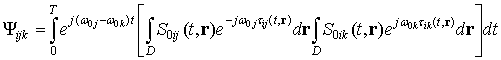Multiposition Synthetic Aperture Radar (MPSAR) 

              Alexander V Ksendzuk 

7. Signal Groups in Multiposition SAR.

7.1. Signal-to-noise ratio in multiposition SAR. Interchannel interference.

In multiposition Synthetic Aperture Radar (MPSAR) interchannel interference effect on radar image quality.  To understand it lets  derive output of the optimal processing algorithm (matching filtering) for the arbitrary bistatic pair “i-th receiver – k-th transmitter”  into signal , noise  and interchannel interference  components .

Signal component is a signal of k-th transmitter, scattered from the surface and received by i-th receiver.

,

where  -radar scene;  -  time of synthesis.

Noise component caused by presence of the additive noise

.

Interference component caused by signals, transmitted by other than “k-th” transmitter, scattered from the surface and received by “i-th” receiver:

.

Signal Groups in Multiposition SAR

Therefore signal-to noise ratio in bistatic pair “i-th receiver – k-th transmitter”

,                                                   (7.1)

significantly depends on interference level

.     (7.2)

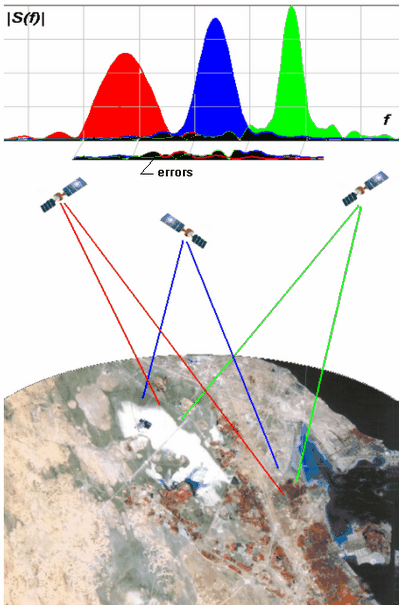
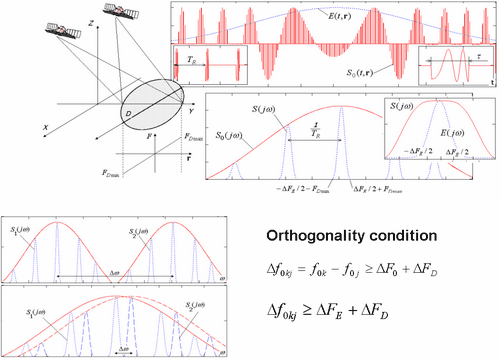
An example of the interference noise in frequency domain is shown in Figure 7.1.

Figure 7.1. Interference noise in multiposition SAR, frequency domain.

For the simplified surface model (See Section 2, equation 2.4 ) interference level (7.2) transforms to

,                                                          (7.3)

where  - radar cross-section in t bistatic pair “i-th receiver – k-th transmitter”,

  - squared interchannel space ambiguity function (meaning of this spatial function will be given later).

7.2. Signal orthogonality in multiposition SAR.

Complex signals  and  (dot above symbol means complex value) orthogonal in classic meaning if condition  satisfied.

In multiposition SAR (MPSAR) this criterion is not sufficient because of  spreading signal spectra caused by scattering from the surface and crafts movement. This means that we need to modify term  “orthogonality”.

Signals of k-th and j-th transmitters we will cal point-orthogonal in i-th receiver if condition

,                                           (7.4)

where ,  - point signals in bistatic pairs “i-th receiver – j-th transmitter” and “i-th receiver – k-th transmitter”, correspondingly.

Function (7.4) is an interchannel space ambiguity function for bistatic pairs “i-th receiver – j-th transmitter” and “i-th receiver – k-th transmitter”, its level allows to estimate errors, caused by non-orthogonality of the signals. Investigation of this function is necessary for radar image quality estimation.

Signals of k-th and j-th transmitters we will call orthogonal in surface   in i-th receiver if condition

.                                  (7.5)

for any  satisfied.

7.3. Signal groups in multiposition SAR. Carrier frequency separation.

Signals with carrier frequency separation.

                                                                                                          (7.6)

characterizes by interchannel space ambiguity function

,                          (7.7)

value of which decreases when difference  increases.

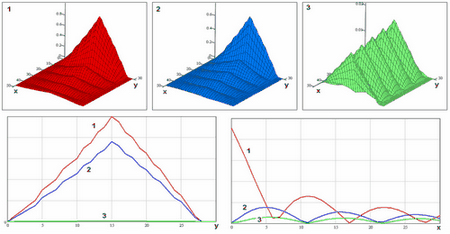
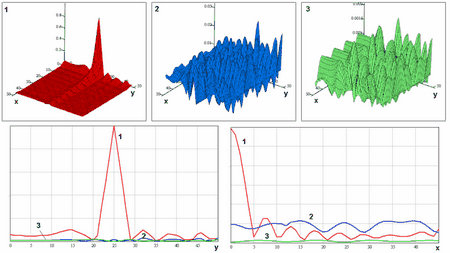
Figure 7.2.  Interchannel space ambiguity function for the signals with different carrier frequencies, difference  increases correspondingly to graph number.

Signals will be orthogonal  if  , where  - bandwidth of the single pulse,   - Doppler bandwidth, Figure 7.3.

 In practice, it is necessary to decrease bandwidth of the MPSAR signal. If condition , where  is a time of pulse repetition satisfied, it is possibly to decrease MPSAR bandwidth, Figure 7.3.

Figure 7.3. Signal and its spectra for the bistatic pair. Orthogonality condition.

7.4. Signal groups in multiposition SAR. Envelope (code) separation.

For the envelope separation signals differ by complex envelope (or buy code for digital signals)

.                                                                     (7.8)

Interchannel space ambiguity function  for the signals with different carrier frequencies

,              (7.9)

can’t be decreased as much as possible only by envelopes (codes) selection, Figure 7.4. But this kind of ensemble allows to decrease MPSAR bandwidth as much as possible.

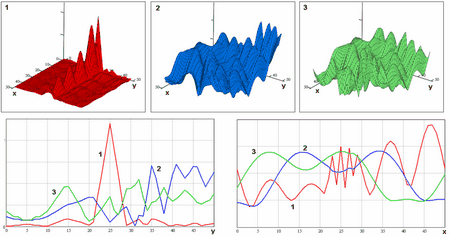
Figure 7.4.  Interchannel space ambiguity function for the signals with different  envelopes.

7. 5. Signal groups in multiposition SAR. Envelope and carrier frequency separation.

For this signal group signals differ by carrier frequency and by envelope (or code for digital signals) simulateneously

.   (7.10)

This kind of separation and corresponding signal ensemble allows to achieve low level of interchannel interference (7.3) and decrease bandwidth of Multiposition SAR signals, Figure 7.5.

Figure 7.5.  Interchannel space ambiguity function for the signals with frequency (graph 1), code (graph 2) and code-frequency (graph 3) separation.

Conclusion.

Signal groups selection in multiposition SAR must be based on signal-to-noise ratio, which takes into account interchannel interference. This interference component of the optimal processor output caused by signals, transmitted by other than “k-th” transmitter, scattered from the surface and received by “i-th” receiver.

Signal groups (carrier frequency separation, envelope separation, carrier frequency and envelope separation) must be chosen for certain MPSAR spatial configuration because value of the interchannel interference depends on  interchannel space ambiguity function, which is depends on spatial configuration. In general case (for signals finite in frequency domain) it is possible to provide orthogonality of the equal signals only by spatial configuration variation.

This means that it is necessary to do simultaneous optimization of the signal groups, and spatial configuration of the multiposition SAR must be based on criteria, which involve interchannel interference (7.3) or  signal-to-noise ratio (7.1):

,  .

top

e-mail to author: Alexander V Ksendzuk